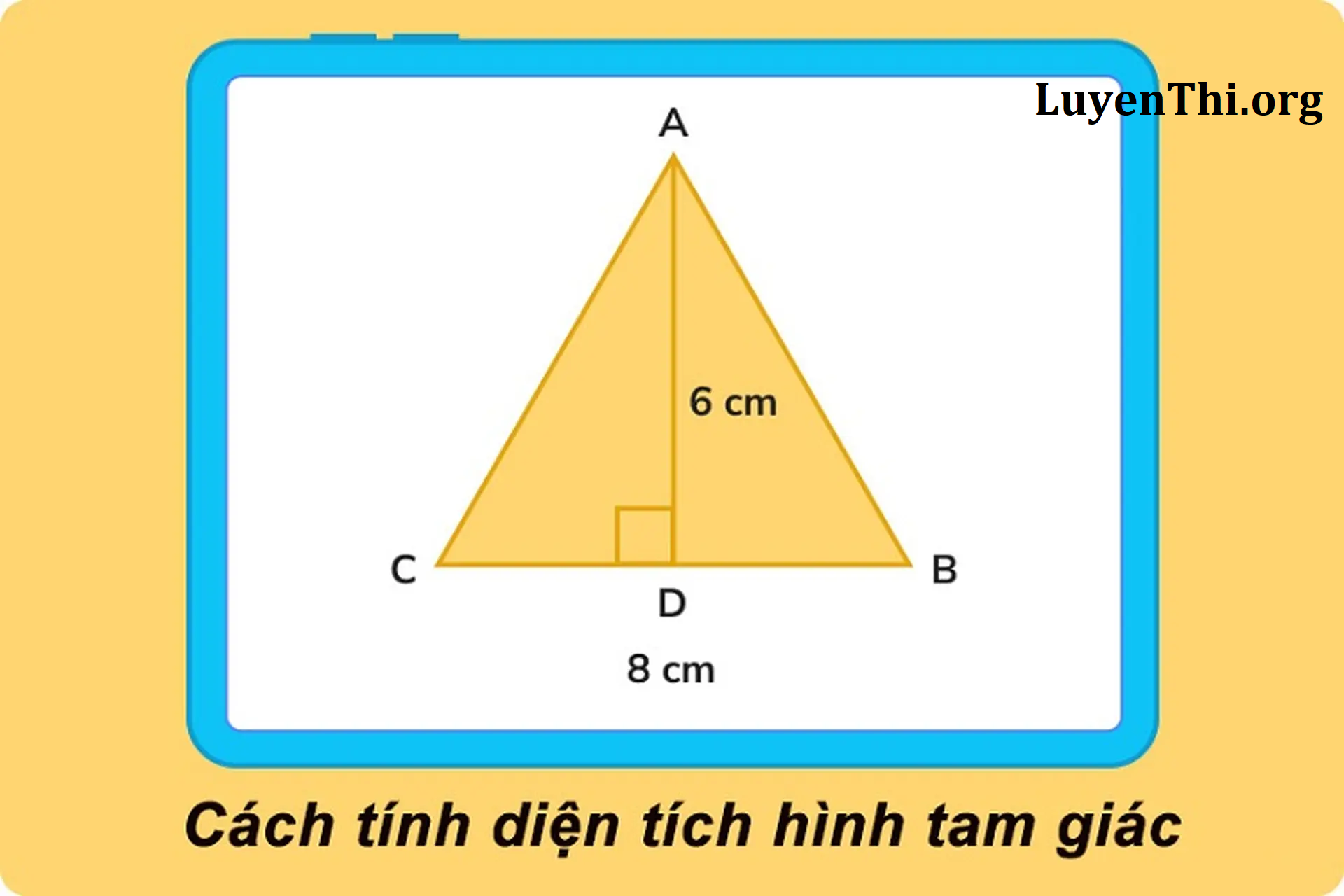
Hiện có nhiều công thức tính diện tích tam giác vuông, thường, cân và đều nên việc chọn công thức nào giúp giải được bài toán đã khó, giải nhanh càng khó hơn. Để tiện tra cứu và học tập thì luyenthi.org sẽ hệ thống đầy đủ những công thức từ căn bản tới nâng cao. Phần bài tập sẽ giới thiệu những bài thường gặp và công thức giải nhanh tương ứng để bạn hiểu sâu.
1. Tam giác là gì?
Tam giác là hình có 3 cạnh và 3 góc, được nối với nhau thành một hình khép kín. Ví dụ: hình giống như một miếng bánh pizza cắt ra!

2. Công thức tính diện tích tam giác
2.1 Diện tích tam giác thường
a. Công thức tổng quát

Trong đó:
- a = BC
- b = AC
- c = AB
- ha, hb, hc lần lượt là đường cao hạ từ đỉnh A, B, C xuống cạnh đối diện BC, AC, AB.
b. Tính diện tích tam giác khi biết một góc

Trong đó: A, B, C lần lượt là các đỉnh của tam giác.
c. Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron.
Cho tam giác ΔABC, các cạnh có độ dài BC = a; AC = b; AB = c thì
Gọi p là chu vi nửa tam giác, khi đó: $p = \frac{1}{2}\left( {a + b + c} \right)$
Công thức heron là
- Diện tích hình tam giác theo nửa chu vi: $S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} $
- Diện tích hình tam giác theo cạnh: $S = \frac{1}{4}\sqrt {\left( {a + b + c} \right)\left( {a + b – c} \right)\left( {b + c – a} \right)\left( {c + a – b} \right)} $
2.2 Tam giác cân
Công thức (nếu biết đáy và chiều cao): $ S = \frac{1}{2} \times a \times h $
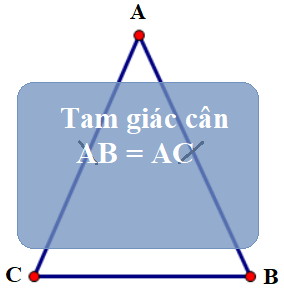
Ví dụ: Tam giác cân có đáy 8cm, chiều cao 5cm $ S = \frac{1}{2} \times 8 \times 5 = 20\text{ cm}^2 $
2.3. Tam giác vuông
Công thức (hai cạnh góc vuông): $ S = \frac{1}{2} \times a \times b $

Ví dụ: Tam giác vuông có hai cạnh góc vuông dài 3cm và 4cm $ S = \frac{1}{2} \times 3 \times 4 = 6\text{ cm}^2 $
2.4 Tam giác đều
Công thức: $ S = \frac{a^2 \sqrt{3}}{4} $
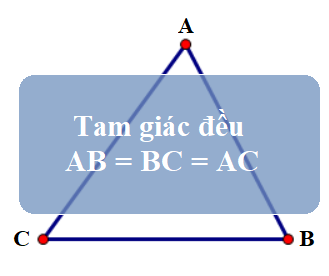
Ví dụ: Tam giác đều cạnh 6cm $ S = \frac{6^2 \sqrt{3}}{4} = \frac{36\sqrt{3}}{4} = 9\sqrt{3} \approx 15.59\text{ cm}^2 $
2.5. Tam giác vuông cân
Công thức (hai cạnh góc vuông bằng nhau): $ S = \frac{1}{2} \times a \times a = \frac{a^2}{2} $
Ví dụ: Tam giác vuông cân cạnh góc vuông 5cm $ S = \frac{5^2}{2} = \frac{25}{2} = 12.5\text{ cm}^2 $
3. Bảng hệ thống các công thức diện tích
| Loại tam giác | Công thức diện tích | Ghi chú |
|---|---|---|
| Tam giác thường | \( S = \frac{1}{2} \cdot a \cdot h \) | a: đáy, h: chiều cao tương ứng |
| Tam giác cân | \( S = \frac{1}{2} \cdot a \cdot h \) | Giống tam giác thường, cần biết chiều cao từ đỉnh |
| Tam giác vuông | \( S = \frac{1}{2} \cdot a \cdot b \) | a, b: hai cạnh góc vuông |
| Tam giác đều | \( S = \frac{a^2 \sqrt{3}}{4} \) | a: cạnh tam giác đều |
| Tam giác vuông cân | \( S = \frac{a^2}{2} \) | a: cạnh góc vuông (2 cạnh bằng nhau) |
| Heron | \( S = \sqrt{p(p – a)(p – b)(p – c)} \), \( p = \frac{a + b + c}{2} \) |
Dành cho tam giác bất kỳ |
| Theo sin | \( S = \frac{1}{2} \cdot a \cdot b \cdot \sin(C) \) | Biết hai cạnh và góc xen giữa |
4. Mẹo nhớ nhanh
- “Vuông” thì lấy 2 cạnh góc vuông
- “Cân” thì cố tìm chiều cao nếu có
- “Đều” thì dùng công thức đặc biệt có căn \(\sqrt{3}\)
Biết công thức tính diện tích tam giác giúp em tính nhanh và đúng diện tích của nó, ví dụ khi cần đo đất hay vẽ hình. Nó giống như công cụ giúp em giải bài toán dễ hơn!